Droites parallèles

Définition

Définition :
Deux droites sont dites parallèles si elles possèdent un vecteur directeur en commun

(Droite)

Notation

On note $D_1\;||\;D_2$ si les droites $D_1$ et $D_2$ sont parallèles

Caractérisation

Proposition :
Deux droite $\{a_1x+b_1y=d_1\}$ et $\{a_2x+a_2y=d_2\}$ sont parallèles si et seulement si $$(a_1:b_1)=(a_2:b_2)$$

Propriétés

Direction

Construction

Exercices

Consigne: $ABC$ est un triangle, $O$ est un point de $(BC)$
Par $B$ et $C$, on trace respectivement deux droites parallèles $d_1$ et $d_2$
La parallèle à $(AC)$ passant par $O$ coupe $d_1$ en $I$, et la parallèle à $(AB)$ passant par $O$ coupe $d_2$ en $J$
Montrer que $A$, $I$ et $J$ sont alignés
(on peut se restreindre au cas où $A$ est entre $d_1$ et $d_2$)

Schéma

Poser $\varphi$
Soit $I\in d_1$, soit $O$ tel que $(OI)//(AC)$ et $O\in(BC)$
Soit $J\in d_2$ tel que $(OJ)//(AB)$
L'application $\varphi:I\mapsto J,d_1\to d_2$ est affine (composée de $2$ projections parallèles) $$d_1\overset{//(AC)}\longrightarrow(BC)\overset{//(AB)}\longrightarrow d_2$$

$\varphi$ est une homothétie
$\overrightarrow{I_BI_C}$ et $\overrightarrow{J_BJ_C}$ n'ont pas le même sens, donc $\varphi$ n'est pas une translation
$\Rightarrow$ c'est une homothétie

Son centre est $(I_BJ_B)\cap(I_CJ_C)=(AB)\cap(AC)=A$
Donc $A,I,J$ sont alignés
4: Centre de l'homothétie

(Translation, Homothétie)

Consigne: Soit $\triangle ABC$ un triangle et $\mathcal C$ son cercle circonscrit, de centre $O$
Soit $A^\prime$ le point diamétralement opposé à $A$ sur le cercle $\mathcal C$
La hauteur $(AH)$ issue de $A$ du triangle $\triangle ABC$ recoupe le cercle $\mathcal C$ au point $D$ ($A$ et $D$ sont distincts)
Si $D\ne A^\prime$, on note $\mathcal D=(DA^\prime)$, sinon $\mathcal D$ désigne la tangente à $\mathcal C$ en $D=A^\prime$
Montrer que la droite $\mathcal D$ est parallèle à $(BC)$

Ce qu'il faut montrer + schéma du premier cas
Montrons d'abord que $\mathcal D\perp(AH)$ dans les deux cas
1er cas :

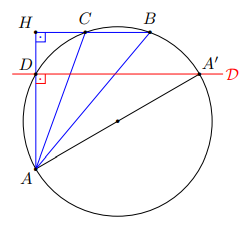
1er cas : angle inscrit éclaire un demi-cercle
Si $D\ne A^\prime$, alors comme $AA^\prime$ est le diamètre du cercle, l'angle inscrit $\measuredangle ADA^\prime$ éclaire un demi-cercle, et donc $\measuredangle ADA^\prime=\frac\pi2$
Ainsi $\mathcal D\perp(AH)$

Schéma du 2e cas

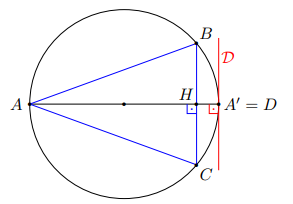
2e cas : tangente est perpendiculaire à un diamètre $\to$ à $(AH)$ car les points sont alignés
2e cas : si $D=A^\prime$, alors comme $AA^\prime$ est un diamètre et $\mathcal D$ est tangente en $A^\prime$, nous avons $\mathcal D\perp(AA^\prime)$
Ainsi, comme dans le cas précédent, $\mathcal D\perp(AH)$ car $A,A^\prime=D$ et $H$ sont alignés

Conclusion : deux droites perpendiculaires à une même droite sont parallèles

Pour conclure, vu que $\mathcal D\perp(AH)$ et $(AH)\perp(BC)$ comme hauteur, nous avons $\mathcal D\;||\;(BC)$